

SEARCHING FOR THE ULTIMATE ANSWER...
PQR THEORY
UNREAL NUMBERS, PART II
As we saw in Part I of this article, mathematicians define the infinitesimally small “gaps” in the Rational numbers to be “Irrational numbers” which, taken together with the Rational numbers, constitute the so-called Real number line.
The Real numbers can be defined in a number of broadly equivalent ways. One commonly used definition says that a Real number represents a separation of the Rational numbers into two sets A and B, where all the numbers in set A are smaller than all the numbers in set B. For instance, √2 can be defined by taking set A to be all the Rational numbers that are negative or whose squares are less than 2, and set B to be all the positive Rational numbers whose squares are greater than 2. (Note that in this case there is no “largest” Rational number in set A and no “smallest” Rational number in set B.) It can be proved that this definition uniquely specifies the Irrational number that occupies the gap “between” the two separated groups of Rational numbers. (In the special case where set A has a “largest” member or set B has a “smallest” member, i.e. a Rational number x that is greater or smaller than all the other Rational numbers in its set, this definition gives us the Rational number x as a member of the Real numbers.)
From the way they are constructed you might imagine that, as you go along the number line, the Real numbers are alternately Rational and Irrational. But you would be wrong, because we are dealing with the infinitesimal. There are infinitely many Irrational and Rational numbers to be found, in even the shortest section of the number line, and there is no sense in which any two Real numbers are “next to” each other. In fact it turns out that among the Real numbers, the Irrational numbers are vastly more common than the Rational ones. (One way to appreciate this is to notice that the decimal expansion of any Rational number must eventually terminate or go into a finite loop, whereas the decimal expansion of any Irrational number goes on for ever. Compared to Rational numbers, Irrational numbers have a lot of extra digits, which is why there can be so many more of them.)
Mathematicians are quite satisfied with this state of affairs, even though you might find it to be strange and surprising. Yet in constructing the Real numbers from the Rational numbers, they have made a tacit assumption which, on close examination, I believe is unwarranted.
This assumption is known as the Axiom of Choice. Broadly speaking, this says that you can make an infinite number of selections in a finite amount of time. For example, you are permitted to choose the infinite sequence of digits that describes a Real number. (Or equivalently, that you can choose which members of the infinite set of Rational numbers are in Set A and which are in Set B.) While this Axiom is attractive and intuitive, its truth is by no means obvious, and mathematicians know that they cannot prove it. But since they need it in order to support a lot of interesting results in set theory and other branches of mathematics, they call it an Axiom, which is just another way of saying that because they can’t prove it, they’ll assume it to be true.
PQR theory, however, states that the Axiom of Choice, while it may be of theoretical interest to logicians, has NO APPLICATION to our physical Universe. This is for the simple reason that the Axiom of Choice says you can create an infinite amount of information, but our Universe can only hold a finite amount of information.
The consequences of this are far reaching but may be summarized as follows:
1. The so-called “Real” numbers are a misnomer. Arbitrary Irrational numbers have no physical reality and are not required or used in the physical laws that govern our Universe.
2. The so-called “Space-Time Continuum” does not exist. Space and time are not infinitely divisible, so they cannot be continuous. (In fact, as will be discussed in another article, it is even questionable whether Space-Time would have any existence at all in the absence of matter and energy.)
This does not mean that our theories about the physical Universe are completely wrong. But we must be aware that the formulae and tools we use to describe its workings (which we call the Laws of Physics) are not the ultimate truth about the Universe, but merely reflect an approximation to its underlying workings. In particular, the so-called “real-number line” that we use as the basis for our models of space and time can never be truly continuous in our finite Universe, but must contain gaps. Furthermore these gaps, though small, are of finite size (and thus much bigger than the infinitesimal gaps in the Rational numbers). The spacetime in which we exist is not infinitely divisible, but only divisible to the extent allowed by the numbers which comprise our Universe. These numbers, although enormous, are nevertheless finite, which means that space and time, although they have a very fine structure, are not completely smooth. They are more like a fluid which appears to be smooth but, on very close examination, is found to be composed of discrete molecules.
Thus, although irrational numbers like π, e and √2 may be widely used in mathematicians’ and physicists’ formulae, these formulae only give us approximations to the Natural numbers that underlie both the geometry of spacetime and the experiments upon which the physicists have based their formulae. And although it may be very convenient for mathematicians and physicists to treat space and time as continuous, this is only an approximation to the true, discrete, nature of our Universe.
An example may help to illustrate this subtle concept. Supposing we have a large piece of graph paper that is marked into 1-millimeter squares. We are allowed to mark these squares, but each little square must be marked in its entirety or not at all. We can measure the distance between two squares, but only in whole millimeters. (We do this by counting the number of horizontal and vertical lines between the two squares. Calling these numbers x and y, we then use the Pythagorean formula √(x²+y²) for the distance, rounding the result down to the next lower whole number). We want to find the area inside a circle of given radius r millimeters. We can do this by marking one square on the paper as the center of the circle, marking all the other squares whose distance from the center (measured as above) is less than r, and then counting the total number of marked squares, as shown in the pictures below. (Notice that we have not used a ruler or compass to make this construction, we have done it by counting and arithmetic only.)

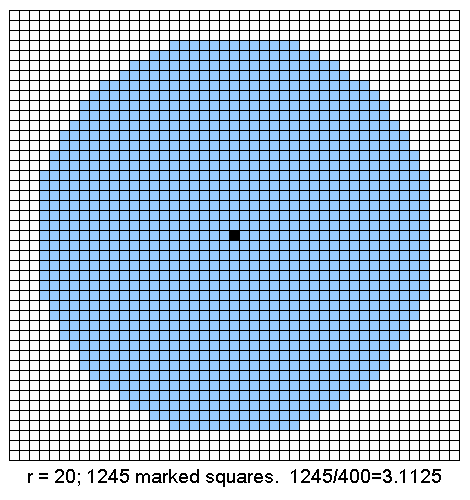
This gives us the exact area in square millimeters of the (roughly circular) region of the paper that we have marked. This number will be approximately π times r², so if we divide the area by r² we can obtain an estimate for π. (This estimate will be a Rational number as long as r was also one). The larger we make our circle (or the smaller we make our squares), the closer to a true circle will our marked region tend to be, and the more accurate will our estimate for π tend to become, as shown by the examples below.
Now imagine that this graph paper represents a two-dimensional world in which space is discrete, i.e. each little cell on the graph paper represents an indivisible unit of space, a space which can only be subdivided along the lines that separate the cells. If there were mathematicians living in this graph-paper Flatland, they could in principle perform the same calculations and compute π to any degree of accuracy they desired. They would then, like us, be able to say “the area of a circle is the square of its radius times 3.14159265...”. But they would be wrong. In the discrete integral space of the graph-paper world, there are no fractional areas, and the regions that look like circles are really made up of small squares. Although mathematically π is an exact constant, the true area of the marked region is only approximately given by the exact formula π r ².
In the same way, our physical laws, though they might be exactly accurate if space and time were infinitely divisible, can only approximately predict the actual results of any experiment (which of course will always be expressed in terms of Rational numbers). Although these approximations may be very close, there will always be experimental errors. Physicists often ascribe part of these errors to “quantum effects,” which is really just another way of saying that their continuous-formula theories can, at best, only approximate to reality. Their formulas are based on an idealized universe in which space and time are continuous, but our real Universe only approximates to this theoretical model. When we examine things at the subatomic level, our Universe is well known for its unpredictable behavior. Perhaps this “quantum weirdness” does not arise from the nature of matter and energy as physicists have assumed, but from the nature of numbers, space and time.
Nick Mitchell, January 2009